In this article, we will go over what is a function and the different types of functions.

1 Terminologies

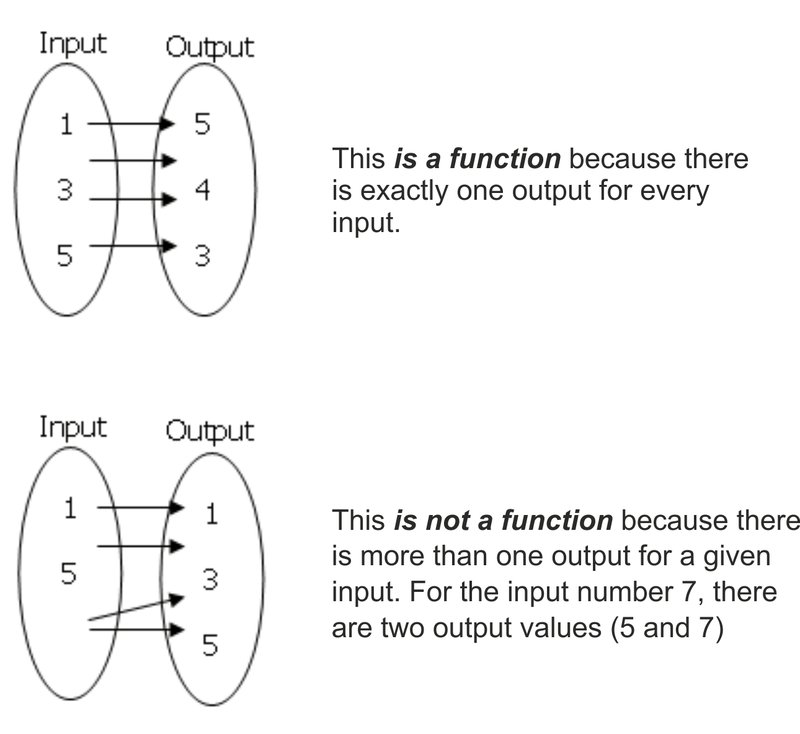
• A function $f$ from $A$ to $B$, denoted as $f : A → B$, is a relation from $A$ to $B$ that assigns each element of $A$ to exactly one element of $B$.
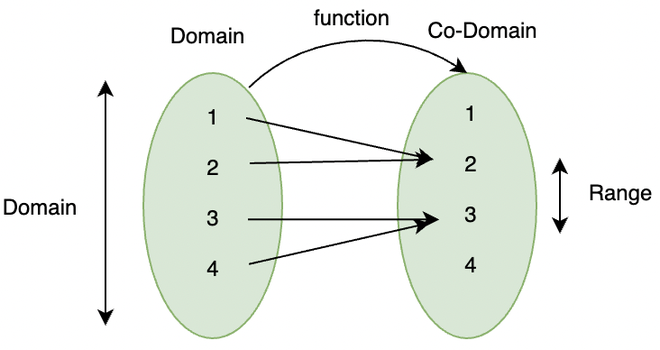
• $A$ is called the domain of $f$. The domain is the set of all inputs.
• $B$ is called the codomain of $f$. The codomain is the set of all allowable outputs.
• If $f$ maps element $a∈A$ to element $b∈B$, we write $f(a)=b$.
• If $f(a)=b$, $b$ is an image of $a$ and $a$ is a preimage of $b$ .
• The range of $f$ is the set of all images of elements in $A$.

1. Identifying a function

2. Difference between codomain and range

2 One-to-one functions

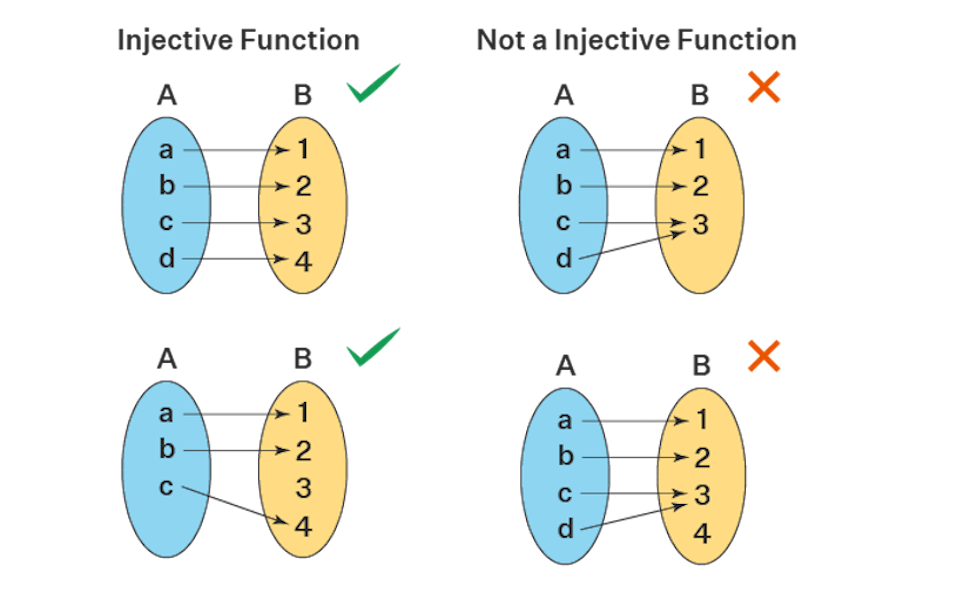
A function $f(x)$ is called one-to-one or injective if and only if $f(x)=f(y)$ implies $x=y$ for every $x$, $y$ in the domain of $f$. In other words, one-to-one functions never assign different elements in the domain to the same element in the codomain.

2.1 Proving injectivity

There are a few methods to check if a function is injective:

1. Arrow diagram

We can draw arrow diagrams that represents the mapping of the relations from the domain to codomain in order to determine if the function is injective or not. However, this method is very difficult to use when the domain and codomain is large.

2. Horizontal line test

This method is easy and convenient. All we have to do is draw a horizontal line through the graph of a function and if it intersects the graph only once, then the function is one-to-one as shown in the example below:

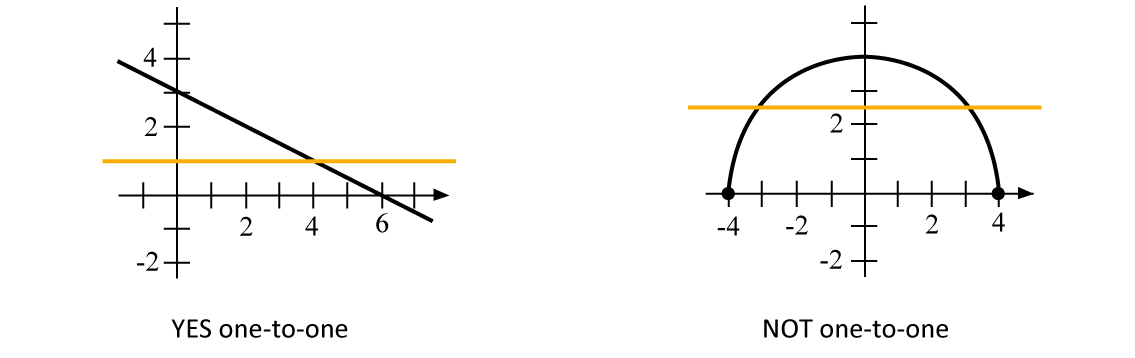
However, this method only works for graphs over real numbers.

3. Mathematical proof

This is the most commonly used method for proving injectivity as it is more general and straightforward.

Steps:

1. Assume $f(a)=f(b)$ for all $a$, $b$ in the domain.
2. Some workings to show that $a=b$
3. Conclude that if $f(a)=f(b) → a=b$, then $f(x)$ is injective

Example:

3 Onto functions

A function $f$ is called onto or surjective if and only if for every element $y$ in the codomain, there is an element $x$ in the domain such that $f(x)=y$. In this case, the range of $f$ is equal to the codomain.

3.1 Proving surjectivity

There are also multiple ways to see if a function is surjective:

1. Arrow diagram

We can also use the arrow diagram method to prove surjectivity but same limitations apply.

2. Comparing range and codomain

If we are given a graph, the easiest way to determine surjectivity is to compare the range with the codomain. If they are the same, then the function is surjective.

3. Mathematical proof

The key to proving a surjection using the proof method is to figure out what we’re after then work backwards from there.

Example: Prove that f(x) = x - 8 is a surjective function for any integer x.

Assume for any $y∈ℤ$, there exists an $x∈ℤ$ such that $x=y+8$.

Then $f(x) = (y+8)-8 = y$ by definition of $f(x)$.

Hence $f(x) = y$ for all $x$, $y$ and $f$ is onto.

4 Bijective functions

A function is bijective if it is both injective and surjective. To prove the bijectivity of a function, we have to prove both injectivity and surjectivity. Here’s a diagram to summarise what we have learnt so far:

4.1 Functions and cardinality

Given that $A$ and $B$ are finite sets, the function $f : A → B$ is:

• injective if $|A| ≤ |B|$,
• surjective if $|B| ≤ |A|$,
• bijective if $|A| = |B|$.

5 Inverse functions

Every bijection from set $A$ to set $B$ also has an inverse function.

• The inverse of the bijection $f$ is denoted as $f$^-1.
• The inverse function assigns an element $a∈A$ to an element $b∈B$ such that $f(a)=b$.

• A function that has an inverse is called an invertible function.
• A function is invertible if and only if it is bijective. This is because the inverse will not fulfil the criterias of a function if it is not both injective and surjective.

6 Function composition

Let $g$ be a function from $A$ to $B$, and $f$ from $B$ to $C$. The composition of $f$ and $g$, denoted as $f◦g$, is defined by:

• $(f ◦ g)(x) = f (g(x))$

Example 1:

Let $f$ and $g$ be functions from $ℤ$ to $ℤ$ such that $f(x)=2x+3$ and $g(x) = 3x + 2$.

$(f ◦ g)(x) = f (g(x)) = 2(3x+2) + 3 = 6x+7$

Example 2:

Prove $f$⁻¹ $◦ f = I$, where $I$ is the identity function. The identify function for A, written as $I$_A: $A → A$, is defined by $I$_A$(a) = a$ for all $a∈A$.

• Note that $I$_A$(x)$ = $x$.

• $(f$⁻¹ $◦ f)$$(x)$ = $f$⁻¹$ (f(x))$

• Let $f(x)$ be $y$.

• Then, $f$⁻¹$ (f(x))$ = $f$⁻¹ $(y)$.

• By definition of inverse, $f$⁻¹ $(y) = x$ if and only if $f(x) = y$.

• Thus, $f$⁻¹$ (f(x))$ = $f$⁻¹ $(y)$ = $x$ = $I$_A.